June 2017, updated September 2020
SetLoop – iterator plugin for Nuke
SetLoop is a toolset for Nuke that I made, it can loop a set of nodes a certain amount of times!
It copies the nodes you place between StartLoop and EndLoop inside the group EndLoop, and reconnects them properly.
There are many more features to it which, combined, make this an actually functional node iterator that can render fractals (like the Mandelbrot and the Julia Set) and animated reaction diffusion entirely in Nuke.
Both 2D and 3D nodes can be looped:


All examples on this page are included in the download!

Since it automates creating a lot (in most cases, hundreds) of nodes, there are some automatic relinking options for external nodes, or references in TCL expressions.
There is also an option to create a knob (‘iteration’) on every node in the loop, with an integer counting the current loop’s iteration.
This knob can then be referenced in expressions to get unique values for each loop iteration.
All features explained:
- loops
amount of loops to create - method
– sequential loops like an iterator
– parallel creates multiple instances of the same input and merges them together
– geometry is like parallel but for geo - build method
– in this group node (live)
copies the nodes to loop over into this group node for a live loop within Nuke
– iterations to exr (baked)
keeps the group empty and writes each iteration as a sequence on top of an exr of the previous one, faster but not live - relink external inputs
relink nodes that are not in the loop via extra inputs in this group node - relink external expressions
attempt to fix expressions when they’re moved into this group by:
changing ‘parent.’ to ‘root.’ when the nodes they refer to are not in the loop
adding ‘root.’ in expressions before nodes that are not within the loop
changes are only made to nodes in the loop itself, and they will be printed in the script editor panel - remove ‘parent.’
automatically removes the ‘parent.’-part for all expressions on nodes in the backdrop, which often fixes common relinking issues
make a copy of the nodes in the backdrop before setting the loop with this enabled, as it permanently alters the expressions on knobs
all changes will be printed in the script editor panel - add iteration knob
add a knob called ‘iteration’ to all nodes in the loop, with an integer value representing their looping index
the original nodes (the ones in the backdrop in the main graph) will also get this knob, starting at 0 - set
bake the loop (or clear it when it is empty) - scroll
animate the loop level - invert
invert the direction of the scroll
– only available with method parallel - blend
blends the loop levels when scroll is not a round number - spread
feather the loop levels
– only available with method parallel and blend enabled - operation
the merge operation to use
– only available with method parallel - offset
offset the loop count knob value
– only available when iteration knob is enabled and set - [tab] Custom
room for custom knobs that can be referenced to from in the loop
Normal installation
1. Place the SetLoop folder in your .nuke folder (or somewhere else on your computer)
Linux: /home/username/.nuke
Mac: /Users/username/.nuke
Windows: C:\Users\username\.nuke
2. Go to your .nuke folder, and create a file called ‘init.py’. If such a file already exists, open it.
3. In the init.py file, add this line of text to the end and save it:
nuke.pluginAddPath(‘./SetLoop’)
Installation using NukeShared
1. Place the SetLoop folder in the ‘_AutoInstaller’ repository.
NukeShared is a way of installing plugins by dragging/dropping them in folders, see this page for more information.
Reaction Diffusion
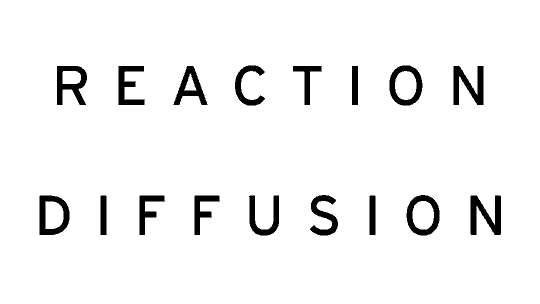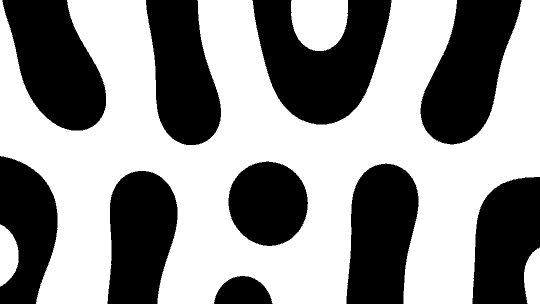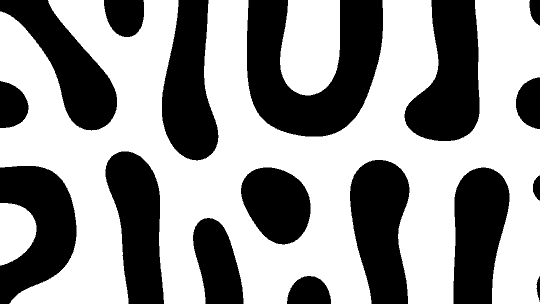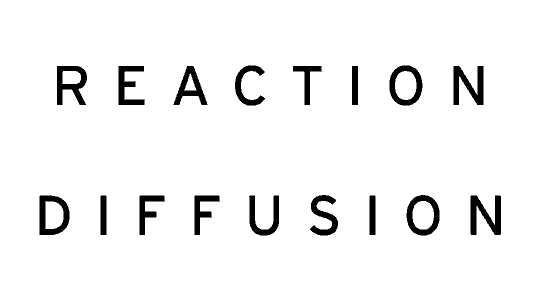
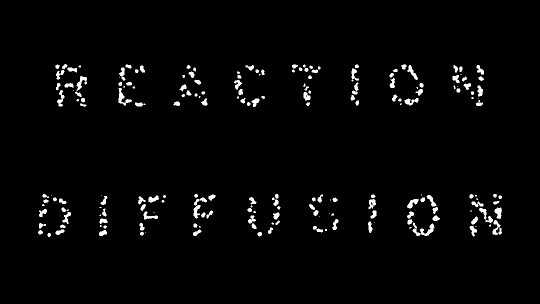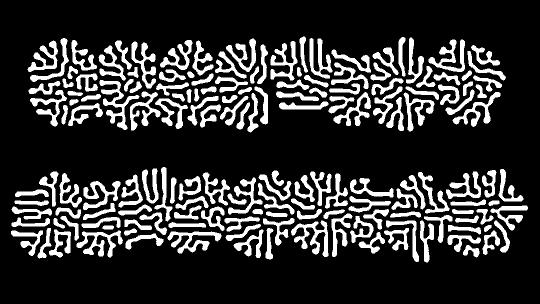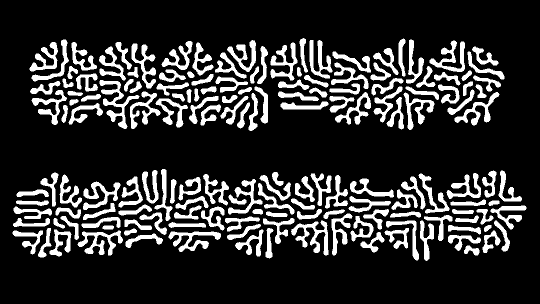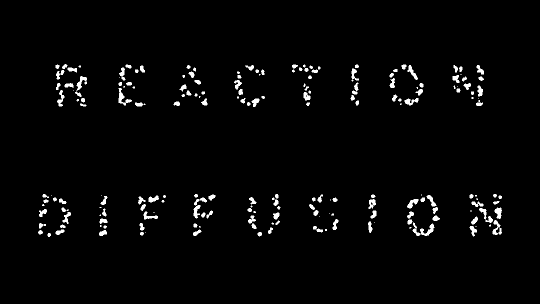
Reaction Diffusion is often referred to as a chemical process that describes how dots and stripes in the skin of animals are formed.
I made a simple version of this effect in Nuke, by subtracting two different blurred versions of the same image from each other.
Doing this about 150 times will result in some really cool patterns (and the loop level can also be animated using ‘scroll’ parameter).
The iteration process is done using SetLoop and the node graph looks like this:
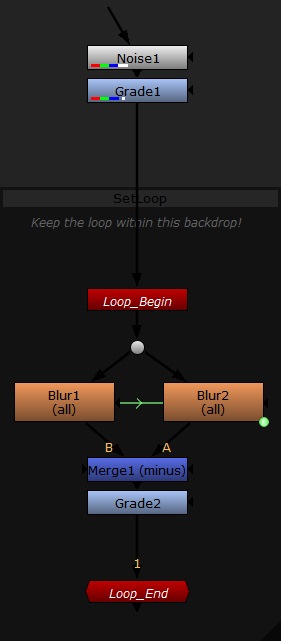
Blur2.size has an expression that makes it three times the size of Blur1.size.
Using the ‘iteration’ feature can give some interesting results, and external expression re-linking can be used to set all blurs in the loop to be the same size at once.
This is a before-and-after of Reaction Diffusion with different inputs:


The Mandelbrot Set






The Mandelbrot set is an amazing set of numbers. The trick is to iterate an Expression node as often as possible over the same pixels.
This iteration process is where SetLoop comes in handy.
First, let’s get a good understanding of the mathematics behind a Mandelbrot set. After that, we’ll look at how to integrate that in Nuke.
The Mandelbrot set uses complex numbers. Complex numbers can be thought of as numbers that are in a two-dimensional number system. Like coordinates!
They consist of a ‘real’ number (a) and a ‘complex’ number (b), and are then noted as a + bi.
For me, it helps as thinking of them as ‘x’ and ‘y’ coordinates sometimes.
The horizontal axis on this coordinate plane is where the real numbers (1, 2, 3) are. The vertical axis shows the ‘extra dimension’ of complex numbers that can be added.
The three example coordinates P_1(-2,-2i), P_2(1,-1.2i) and P_3(2,2i) are highlighted:

The i is a symbol telling us that the second number is a complex number, but it is also a number itself: i = \sqrt{-1} (and thus i^2 = -1).
This wouldn’t be possible using only real numbers. Khan Academy has some cool visualisations of complex numbers and their behaviour, which also show the importance of visualizing them on a coordinate plane.
Now, what exactly is the Mandelbrot set?
Let’s take the coordinate system of the real and complex numbers as an image with coordinates (x, y) to draw on.
The basis of the Mandelbrot is this very short equation:
Z_n = Z_{n-1}^2 + C
Z = a complex number, initially equal to C
C = a complex number and constant
As you can tell from the Z repeating itself, this is just one iteration. After this is calculated many times, the result can be measured to be smaller or bigger than 2 (to check if it has ‘blown up’ or not).
Make the values that are bigger than 2 a different color from the ones that aren’t, and you’ll have a Mandelbrot set.
Why 2?
Addition and multiplication with complex numbers is following the standard arithmetic rules, but the format in which they’re written ((a + bi) – or, since we’re using them in a coordinate system: (x + yi)) should be maintained:
Addition:
(x_1 + y_1i) + (x_2 + y_2i)
= x_1 + x_2 + y_1i + y_2i
= (x_1 + x_2) + (y_1 + y_2)i
Multiplication:
(x_1 + y_1i) * (x_2 + y_2i)
= x_1x_2 + y_1x_2i + x_1y_2i + y_1y_2i^2
= (x_1x_2 - y_1y_2) + (x_2y_1i + x_1y_2i)
= (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i
Let’s plug our x + yi in the equation of Z (where C = x_0 + y_0i, as this constant is the first value)
Z = (x + yi)^2 + (x_0 + y_0i)
= (x + yi)(x + yi) + (x_0 + y_0i)
= (x^2 - y^2) + (2xy) + (x_0 + y_0i)
= (x^2 - y^2 + x_0) + (2xy + y_0i)
Now split this result in two – the real, and the complex part:
(x^2 - y^2 + x_0) and (2xy + y_0i)
This explains why Z cannot exceed 2. Let’s have C = -2, to simulate what happens if Z = 2:
Z_n = Z_{n-1}^2 + -2:
Z_{(0)} = 0 (first iteration)
Z_{(1)} = 0^2 + -2 = -2
Z_{(2)} = -2^2 + -2 = 2
Z_{(\infty)} = 2^2 + -2 = 2
This will stay at 2 forever. Only if Z^2 > 4, Z will approach infinity.
After many iterations, Z = \sqrt{4} = 2 will be unlikely, except if it is in the Mandelbrot Set.
Now we have the equations for both the real and the complex part, we can finally throw this in Nuke.
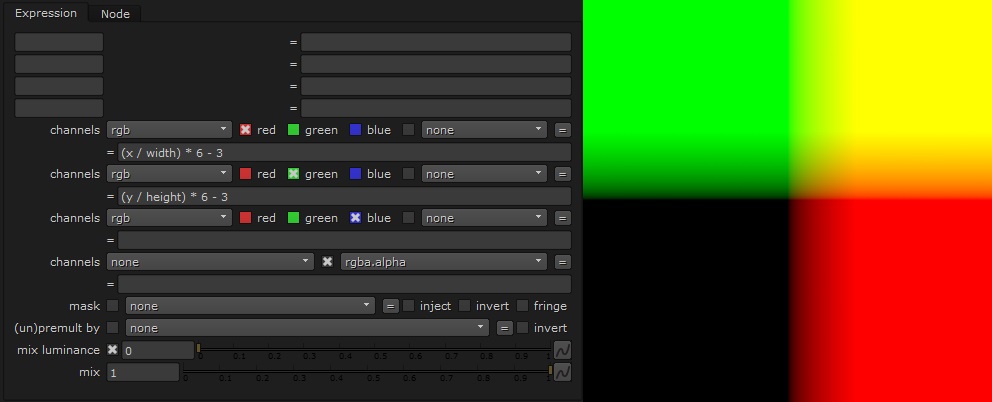
Let’s start by recreating the coordinate system (-3 to 3 in both directions).
The red channel will represent all the real numbers, while the green channel represents the complex numbers.
Add an Expression node that does this:
Add a MergeExpression after that, with both A and B connected to Expression1, which makes the first iteration of the Mandelbrot.
It begins with a variable checking whether\sqrt{Br^2 + Bg^2} < 2.
Then, if that variable (‘valid’, I called it in the expression) is true, switch x, y with Br, Bg (red and green from input B) in the first part (the ‘real numbers’-part) of Z, and set the new red value:
Br * Br - Bg * Bg + Ar
Ar is the ‘original’ red from input A, which won’t be the same after multiple iterations.
If valid is not true, do not change it, but leave it at Br.
To recap: we’re basically using (x^2 - y^2 + x_0) (from a few steps earlier, function Z) in Nuke now!
For the green channel we’re doing the same, except this is the complex part of Z, so it will be:
Br * Bg * 2 + Ag
(Except if valid is false, in which case we won’t change green at all)
One final adjustment: we also want to know how many iterations it took to calculate whether or not a pixel is inside the Mandelbrot. Let’s add that to the alpha, by adding 1 every time valid is true and leaving it when valid isn’t true.
This is what that would look like:
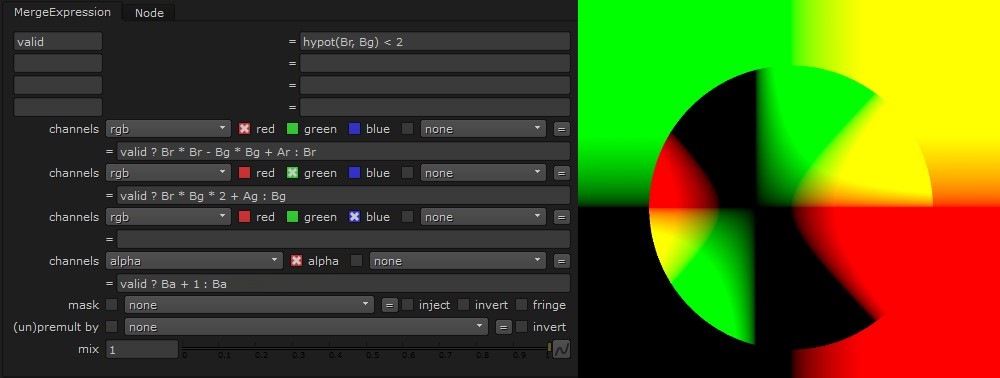
We’re done! This is a visualized Mandelbrot set. Now we just needs to loop this a hundred times.
Let’s make that happen using SetLoop, as I’m not feeling like ctrl+V’ing and reconnecting those nodes.
Add SetLoop to the comp, move the MergeExpression to the middle of SetLoop, but make sure input A of MergeExpression1 is connected to the original Expression node (we want A to be the original value!) – and don’t forget to make sure ‘relink external inputs’ in EndLoop is enabled, as this makes sure that the MergeExpression can find Expression1 from inside the loop.
Set the amount of loops to 100, and when the comp looks like this, click ‘set’:
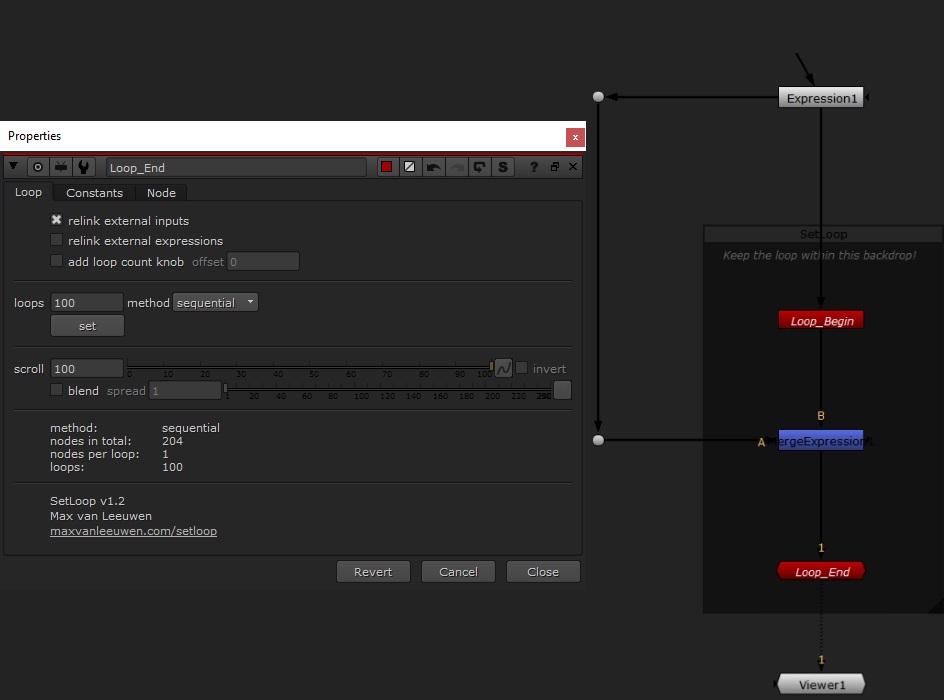
You will have to wait the first calculation out. This might take some time, but once it’s done you can scroll through it pretty smoothly!
You’ll see an extra input for EndLoop was created, to connect the nodes inside the loop.
The RGB result is on the left, and on the right is the alpha divided by ‘EndLoop.loops’ (since we made it add 1 to the alpha per iteration, it should be normalized to the amount of loops to make that visible)

The STMap-node (set to Alpha) can be used to give this Mandelbrot some nice colors, and by multiplying or adding to the width and height in Expression1 the Mandelbrot can be translated and zoomed in on.
Another example included in the download is the Julia Set, which has a variable C component – meaning you can make cool animations with it:


